Incompressible Fluids#
General Introduction#
In CoolProp, the incompressible fluids are divided into three major groups.
The pure fluids and mass-based binary mixtures are by far the most common fluids in this library. While the pure fluids contain data for many different kinds of incompressible liquids, almost all of the binary mixtures are aqueous solutions. For these liquids, the concentration always refers to the added component ranging from 0.0 for pure water to 1.0 for no water at all. Please refer to the tables below to find the allowed minimum and maximum concentrations. Those are likely to be above 0.0 and below 1.0, respectively.
The first entry in the tables below is the fluid ID that can be used to call the
fluid from the high-level interface. A single PDF page showing the fit quality is
linked to that ID in case you would like to see a few more details about any
specific fluid. To get an overview over all the fits, there are also combined
documents with all the
pure fluids and all the aqueous solutions.
You can read more about these reports in a dedicated
section called Fitting Reports.
All incompressible fluids have an arbitrary reference state for enthalpy and entropy. During initialisation, the reference state is defined as a temperature of 20 °C and a pressure of 1 atm according to the U.S. National Institute of Standards and Technology (NIST).
Note
If you use a mixture, the reference state gets updated each time you change the composition. Furthermore, not all temperatures can be used as reference temperature since the fraction \(T_\text{in,1} / T_\text{in,0}\) occurs in the integral used to calculate entropy. The centered fits have a base temperature and setting \(T_\text{ref}\) equal to \(T_\text{base}\) yields \(T_\text{in,0}=0\:\text{K}\), which obviously is a problem. For non-centred fits, the base temperature is equal to 0 K. Read on below for more details.
Pure Fluid Examples#
Incompressible fluids only allow for a limited subset of input variables. The following input pairs are supported: \(f(p,T)\), \(f(p,h)\), \(f(p,\rho)\) and \(f(p,s)\). Some fluids also provide saturation state information as \(f(Q,T)\) with \(Q=0\). All functions iterate on \(f(p,T)\) calls internally, which makes this combination by far the fastest. However, also the other inputs should be fast compared to the full Helmholtz-based EOS implemented for then compressible fluids.
A call to the top-level function PropsSI can provide: temperature, pressure,
density, heat capacity, internal energy, enthalpy, entropy, viscosity and
thermal conductivity. Hence, the available output keys are: T, P, D,
C, U, H, S, V, L, Tmin and Tmax.
In [1]: from CoolProp.CoolProp import PropsSI
#Specific heat capacity of Downtherm Q at 500 K and 1 atm
In [2]: PropsSI('C','T',500,'P',101325,'INCOMP::DowQ')
Out[2]: 2288.1643758645673
#Density of Downtherm Q at 500 K and 1 atm.
In [3]: PropsSI('D','T',500,'P',101325,'INCOMP::DowQ')
Out[3]: 809.0654931667821
#Round trip in thermodynamic properties
In [4]: T_init = 500.0
In [5]: P_init = 101325
In [6]: D_init = PropsSI('D','T',T_init,'P',P_init,'INCOMP::DowQ')
In [7]: S_init = PropsSI('S','D',D_init,'P',P_init,'INCOMP::DowQ')
In [8]: H_init = PropsSI('H','S',S_init,'P',P_init,'INCOMP::DowQ')
In [9]: T_init = PropsSI('T','H',H_init,'P',P_init,'INCOMP::DowQ')
In [10]: T_init
Out[10]: 500.0000000000001
#Saturation pressure of Downtherm Q at 500 K
In [11]: PropsSI('P','T',500,'Q',0,'INCOMP::DowQ')
Out[11]: 38091.37403658103
#Minimum temperature for Downtherm Q
In [12]: PropsSI('Tmin','T',0,'P',0,'INCOMP::DowQ')
Out[12]: 238.15
#Maximum temperature for Downtherm Q
In [13]: PropsSI('Tmax','T',0,'P',0,'INCOMP::DowQ')
Out[13]: 633.15
Mixture Examples#
Almost the same syntax can be used for mixtures. Please note that the mixture
interface developed for CoolProp 5 has not been ported to the incompressible
fluids, yet. For now, you have to use the PropsSI function with a special
composition notation. Depending on your fluid, you have to supply either the
mass fraction or the volume fraction as additional
parameter. This is done via the fluid name by appending a dash and the
fraction of the substance other than water. The fraction notation can be in the
form of percent, LiBr-23%, or as a fraction between 0 and 1, LiBr[0.23], which
corresponds to the new mixture syntax in CoolProp v5.
In [14]: from CoolProp.CoolProp import PropsSI
#Density of a lithium bromide solution at 300 K and 1 atm.
In [15]: PropsSI('D','T',300,'P',101325,'INCOMP::LiBr[0.23]')
Out[15]: 1187.5438243617216
#Density of a lithium bromide solution at 300 K and 1 atm.
In [16]: PropsSI('D','T',300,'P',101325,'INCOMP::LiBr-23%')
Out[16]: 1187.5438243617216
#Specific heat capacity of a lithium bromide solution at 300 K and 1 atm
In [17]: PropsSI('C','T',300,'P',101325,'INCOMP::LiBr-23%')
Out[17]: 3101.436382304021
#Specific enthalpy of a lithium bromide solution at 300 K and 1 atm
In [18]: PropsSI('H','T',300,'P',101325,'INCOMP::LiBr-23%')
Out[18]: 21182.70027246687
In [19]: PropsSI('T','H',28627,'P',101325,'INCOMP::LiBr-23%')
Out[19]: 302.3981212987372
Warning
Some mixture function have a non-monotonic behaviour, this can lead to misleading results when using other inputs than \(f(p,T)\). Keep that in mind and implement a way to validate the results you get from these functions. At the same time, mixture solvers are likely to produce errors due to the same reason…
Partial Derivatives#
A limited subset of partial derivatives is available for the incompressible fluids. Currently,
the following inputs are supported by the PropsSI function:
\(\left( \partial \rho / \partial p \right)_{T,x}=0\),
\(\left( \partial \rho / \partial h \right)_{p,x}\),
\(\left( \partial \rho / \partial s \right)_{p,x}\),
\(\left( \partial \rho / \partial T \right)_{p,x}\),
\(\left( \partial h / \partial p \right)_{T,x}\),
\(\left( \partial h / \partial s \right)_{T,x}\),
\(\left( \partial h / \partial T \right)_{p,x}\),
\(\left( \partial s / \partial p \right)_{T,x}\),
\(\left( \partial s / \partial T \right)_{p,x}\),
and their inverse functions.
Note that all partial derivatives require a constant concentration, which is denoted by the
\(x\), but this \(x\) is not included in the derivative string notation for PropsSI:
\(\left( \partial \rho / \partial T \right)_{p,x}\) translates to d(Dmass)/d(T)|P.
Note
You can calculate other properties from the partial derivatives available. At this point, not all derived properties have been implemented even though some of them can be computed like the isobaric expansion coefficient, which would be \(-\left( \partial \rho / \partial T \right)_{p,x}/\rho\).
For more general information on the partial derivatives, please have a look at the documentation for the high level interface.
Fitting Reports#
A file with all fitting reports for the incompressible fluids can be obtained
from here. These reports help you to
get an overview over the different incompressible fluids
included in CoolProp. The reports start with some basic information about
the fluid. The fluid name used in CoolProp is in the title “Fitting Report for FluidName”
and there is also a description of what the fluid actually consists of. The latter
could also be a trade name or a commonly used non-scientific name. The next item
tells you where we got the data from. This
would typically be a data sheet from a manufacturer’s homepage, some other software
database, a scientific publication or experimental data.
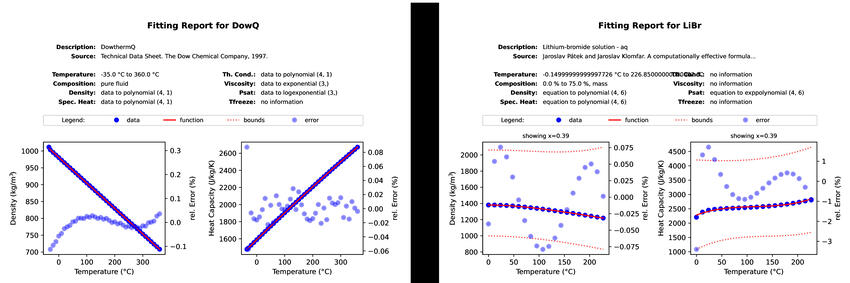
The figure above shows two examples for fitting reports generated for a pure
fluid and a binary mixture. You can also have a look at the
PDF version of the reports side by side.#
If all data are available, there is a graph for each of the basic quantities: density \(\rho\), specific heat capacity \(c\), thermal conductivity \(\lambda\), dynamic viscosity \(\mu\), saturation pressure \(p_\text{sat}\), and freezing temperature \(T_\text{freeze}\). These graphs show data points in dark blue, the fitted function from CoolProp as a red line and the relative error in light blue dots. Note that the relative error uses the ordinate on the right hand side while the other two data series refer to the axis on the left hand side. In case of a solution, these graphs refer to a given concentration that typically lies in the middle of the allowed range. Dashed red lines indicate the limits in terms of concentration as well as the freezing temperature.
Thermodynamics of Incompressible Fluids#
For an incompressible fluid, the specific at constant volume and at constant pressure are the same allowing us to drop the subscripts, \(c_p=c_v=c\). Using temperature \(T\) and pressure \(p\) as state variables, we can simplify the normal thermodynamic relation as described below. working with brines and mixtures, the concentration \(x\) has to be considered as well. Following the same approach as for the compressible fluids, we regard mixtures with different compositions as independent fluids. This should be kept in mind when comparing properties for different compositions. Setting the reference state for one composition will always affect all fluids consisting of the same components.
Note
The internal routines for the incompressibles were updated 2015-02-10, the documentation is not fully updated. We are going to add the new equation as soon as possible, probably mid-March 2015. Please be patient.
According to Melinder [162] and Skovrup [163], using a centred approach for the independent variables enhances the fit quality. Therefore, all solutions have a base temperature and concentration in the original works as well as in CoolProp: \(x_\text{in} = x - x_\text{base}\) and \(T_\text{in} = T - T_\text{base}\), this technique does not affect the calculation of the derived quantity internal energy since the formula contains temperature differences. However, integrating \(c(x_\text{in},T_\text{in})T_\text{in}^{-1}dT_\text{in}\) for the entropy requires some changes due to the logarithm.
Warning
You must not use the base temperature \(T_\text{base}\) as reference temperature for your thermodynamic states. This will lead to an error caused by a division by zero during the integration carried out to obtain the entropy.
To structure the problem, we introduce a variable \(f(j,T)\), which will be expressed by a third sum. As a first step for simplification, one has to expand the the binomial \((T-T_{base})^n\) to a series. Only containing \(j\) and \(T\), \(f\) is independent from \(x_\text{in}\) and can be computed outside the loop for enhanced computational efficiency. An integration of the expanded binomial then yields the final factor \(F\) to be multiplied with the other coefficients and the concentration.
Equations#
There are only four different equations used to calculate the thermophysical properties of incompressible fluids in CoolProp:
Only the last two are suitable for mixtures with the input parameter \(x\) denoting the fraction of component other than water. Following the works of Melinder [162] and Skovrup [163], the exponents for the polynomials are arranged in a triangular matrix to avoid overfitting. These conditions satisfy \(0 \leq i \leq n\), \(0 \leq j \leq m\) and \(i + j \leq \max(n,m)\). It is only for the freezing temperature calculation that the implemented procedures differ from what is presented in Melinder’s book [162]. Freezing temperature is only a function of concentration and the dependency on the fluid temperature has been removed. For mixtures, \(m=5\) and \(n=3\) are assigned as default values. Omitting the composition term with \(n=0\) yields the pure fluid formulations for which we selected \(l=1\) and \(m=4\).
The standard polynomials are used for the density, heat capacity and thermal conductivity functions, while viscosity, vapour pressure and freezing temperature are exponential functions. For exponential functions of only one variable (\(\mu(T)\), \(p_\text{sat}(T)\), \(T_\text{freeze}(x)\)), we start by fitting the first equation. If the fit quality is poor, we try the second exponential function. The exponential polynomial is used as a fall-back function for single variable fits and it is the only function used for multivariate fits, e.g. \(\mu(T,x)\).
If you would like to know more about the fitting procedures, you can have a look at this Python notebook, which describes the basics of the multivariate polynomial fits employed in this software. Non-polynomial functions are fitted using the minimisation routines accessible through SciPy [164]. For the extremely curious, the Python module CPIncomp contains the source code for the fits used in CoolProp as well as the code to generate the fitting reports. Feel free to browse the code.
The Different Fluids#
The fluids implemented in CoolProp cover a wide range of industrial heat transfer media. This database has initially been developed with refrigeration systems in mind. That is why the majority of fluids are secondary refrigerants with application temperatures close to the freezing point of water. Besides those, there is also incompressible water, high temperature heat transfer oils and a molten salt mixture for extreme temperatures.
Besides the different technical data sheets and calculation tools provided by manufactures, two specific publications provided a lot of data used for the incompressible fluids: Åke Melinder’s book Properties of Secondary Working Fluids for Indirect Systems [162] has inspired both, the work on pure fluids and aqueous solutions. The second major source of inspiration is the SecCool [163] software, which contains data compiled by Morten Juel Skovrup. It is provided free of charge by his employer IPU.
Name |
Description |
Reference |
\(T_\text{min}\) (°C) |
\(T_\text{max}\) (°C) |
\(T_\text{base}\) (K) |
|---|---|---|---|---|---|
Aspen Temper -10, Potassium acetate/formate |
-10.00 |
30.00 |
273.15 |
||
Aspen Temper -20, Potassium acetate/formate |
-20.00 |
30.00 |
273.15 |
||
Aspen Temper -30, Potassium acetate/formate |
-30.00 |
30.00 |
273.15 |
||
Aspen Temper -40, Potassium acetate/formate |
-40.00 |
30.00 |
273.15 |
||
Aspen Temper -55, Potassium acetate/formate |
-55.00 |
30.00 |
273.15 |
||
Acetone, liquid phase at 10 bar |
[3] |
-75.00 |
143.33 |
307.32 |
|
Air, gaseous phase at 1 atm (101325 Pa) |
-75.00 |
250.00 |
360.65 |
||
Diethylbenzene mixture - Dowtherm J |
[162] |
-80.00 |
100.00 |
0.00 |
|
Dynalene SF |
Dynalene, Inc. |
0.00 |
315.00 |
430.65 |
|
DowthermJ |
[166] |
-80.00 |
345.00 |
405.65 |
|
Dowtherm J, Diethylbenzene mixture |
-73.00 |
315.00 |
394.15 |
||
DowthermQ |
[166] |
-35.00 |
360.00 |
435.65 |
|
Dowtherm Q, Diphenylethane/alkylated aromatics |
-35.00 |
330.00 |
420.65 |
||
Ethanol, liquid phase at 10 bar |
-75.00 |
150.69 |
311.00 |
||
Food ash model from the 2006 ASHRAE Handbook based on data from Choi and Okos (1986) |
[167] |
-40.00 |
150.00 |
273.15 |
|
Food carbohydrate model from the 2006 ASHRAE Handbook based on data from Choi and Okos (1986) |
[167] |
-40.00 |
150.00 |
273.15 |
|
Food fat model from the 2006 ASHRAE Handbook based on data from Choi and Okos (1986) |
[167] |
-40.00 |
150.00 |
273.15 |
|
Food fiber model from the 2006 ASHRAE Handbook based on data from Choi and Okos (1986) |
[167] |
-40.00 |
150.00 |
273.15 |
|
Food ice model from the 2006 ASHRAE Handbook based on data from Choi and Okos (1986) |
[167] |
-40.00 |
150.00 |
273.15 |
|
Food protein model from the 2006 ASHRAE Handbook based on data from Choi and Okos (1986) |
[167] |
-40.00 |
150.00 |
273.15 |
|
Food water model from the 2006 ASHRAE Handbook based on data from Choi and Okos (1986) |
[167] |
-40.00 |
150.00 |
273.15 |
|
Dynalene HC10 |
[168] |
-10.00 |
218.00 |
377.15 |
|
Dynalene HC20 |
[168] |
-20.00 |
210.00 |
368.15 |
|
Dynalene HC30 |
[168] |
-30.00 |
210.00 |
363.15 |
|
Dynalene HC40 |
[168] |
-40.00 |
200.00 |
353.15 |
|
Dynalene HC50 |
[168] |
-50.00 |
210.00 |
353.15 |
|
Hydrocarbon blend - Dynalene MV |
[162] |
-80.00 |
100.00 |
0.00 |
|
Hydrocarbon mixture - Gilotherm D12 |
[162] |
-80.00 |
100.00 |
0.00 |
|
Hydrofluoroether - HFE-7100 3M Novec |
[162] |
-80.00 |
100.00 |
0.00 |
|
HFE-7100, Hydrofluoroether |
-80.33 |
64.27 |
265.12 |
||
HYCOOL 20, Potassium formate |
[170] |
-20.00 |
50.00 |
273.15 |
|
HyCool 30, Potassium formate |
[170] |
-30.00 |
50.00 |
273.15 |
|
HyCool 40, Potassium formate |
[170] |
-40.00 |
20.00 |
273.15 |
|
HyCool 45, Potassium formate |
[170] |
-45.00 |
20.00 |
273.15 |
|
HyCool 50, Potassium formate |
[170] |
-50.00 |
20.00 |
273.15 |
|
Hexane, liquid phase at 10 bar |
-75.00 |
165.03 |
318.17 |
||
LiqNa |
LiqNa |
126.85 |
2226.85 |
1450.00 |
|
NBS, Water |
1.00 |
100.00 |
323.65 |
||
Nitrate salt, 0.6 NaNO3 and 0.4 KNO3 |
[172] |
300.00 |
600.00 |
273.15 |
|
Pirobloc HTF-BASIC |
50.00 |
300.00 |
448.15 |
||
Paracryol, Aliphatic Hydrocarbon |
-40.00 |
180.00 |
343.15 |
||
Paratherm CR |
[174] |
-100.00 |
220.00 |
333.15 |
|
Paratherm GLT |
[174] |
-15.00 |
315.00 |
423.15 |
|
Paratherm HE |
[174] |
0.00 |
330.00 |
438.15 |
|
Paratherm HR |
[174] |
-15.00 |
370.00 |
450.65 |
|
Paratherm LR |
[174] |
-85.00 |
230.00 |
345.65 |
|
Paratherm MR |
[174] |
-40.00 |
315.00 |
410.65 |
|
Polydimethylsiloxan 1 - Baysilone KT3 |
[162] |
-80.00 |
100.00 |
0.00 |
|
Polydimethylsiloxan 2 - Syltherm XLT |
[162] |
-80.00 |
100.00 |
0.00 |
|
Paratherm NF |
[174] |
-10.00 |
315.00 |
425.65 |
|
Paratherm NF, Hydrotreated mineral oil |
-10.00 |
320.00 |
428.15 |
||
Syltherm 800 |
Dow Chemical Company - FLUIDFILE Software accessed May 2017 |
-40.00 |
398.00 |
452.15 |
|
Synthetic alkyl benzene - Marlotherm X |
[162] |
-80.00 |
100.00 |
0.00 |
|
Therminol66 |
[175] |
0.00 |
380.00 |
463.15 |
|
Therminol72 |
[175] |
-10.00 |
380.00 |
458.15 |
|
Citrus oil terpene - d-Limonene |
[162] |
-80.00 |
100.00 |
0.00 |
|
TherminolD12 |
[175] |
-85.00 |
230.00 |
345.65 |
|
TherminolVP1 |
[175] |
12.00 |
397.00 |
477.65 |
|
Thermogen VP 1869 |
-80.00 |
20.00 |
273.15 |
||
Texatherm22 |
[177] |
0.00 |
350.00 |
448.15 |
|
Tyfoxit 1.10, Potassium Acetate |
-10.00 |
40.00 |
288.15 |
||
Tyfoxit 1.15, Potassium Acetate |
-20.00 |
40.00 |
283.15 |
||
Tyfoxit 1.20, Potassium Acetate |
-40.00 |
40.00 |
273.15 |
||
Tyfoxit 1.24, Potassium Acetate |
-55.00 |
40.00 |
265.65 |
||
Fit of EOS from 1 bar to 100 bar |
0.00 |
200.00 |
373.15 |
||
SylthermXLT |
[166] |
-100.00 |
260.00 |
353.15 |
|
Syltherm XLT, Polydimethylsiloxan |
-100.00 |
260.00 |
353.15 |
||
Zitrec S10, Potassium formate/Sodium propionate |
-8.00 |
90.00 |
314.15 |
||
Zitrec S25, Potassium formate/Sodium propionate |
-23.00 |
90.00 |
306.65 |
||
Zitrec S40, Potassium formate/Sodium propionate |
-38.00 |
90.00 |
299.15 |
||
Zitrec S45, Potassium formate/Sodium propionate |
-43.00 |
90.00 |
296.65 |
||
Zitrec S55, Potassium formate/Sodium propionate |
-55.00 |
90.00 |
290.65 |
There are also a number of water-based mixtures implemented in CoolProp. Most of them
are secondary heat transfer fluids, but there are also aqueous solutions of
ammonia [162], MAM,
and lithium bromide [180], LiBr,
which can be used to model absorption chillers.
Name |
Description |
Reference |
\(T_\text{min}\) (°C) |
\(T_\text{max}\) (°C) |
\(T_\text{base}\) (K) |
\(x_\text{min}\) |
\(x_\text{max}\) |
|---|---|---|---|---|---|---|---|
Freezium, Potassium Formate |
-40.15 |
39.85 |
273.15 |
0.19 |
0.50 |
||
Ice slurry with Ethanol |
-33.15 |
-8.15 |
252.50 |
0.05 |
0.35 |
||
Ice slurry with NaCl |
-18.15 |
-3.15 |
262.50 |
0.05 |
0.35 |
||
Ice slurry with Propylene Glycol |
-43.15 |
-8.15 |
247.50 |
0.05 |
0.35 |
||
Lithium-bromide solution - aq |
[180] |
-0.15 |
226.85 |
386.50 |
0.00 |
0.75 |
|
Ammonia (NH3) - aq |
[162] |
-100.00 |
30.00 |
268.50 |
0.00 |
0.30 |
|
Melinder, Ammonia |
-49.00 |
20.00 |
258.65 |
0.08 |
0.24 |
||
Calcium Chloride (CaCl2) - aq |
[162] |
-100.00 |
40.00 |
280.68 |
0.00 |
0.30 |
|
Melinder, Calcium Chloride |
-44.00 |
30.00 |
266.15 |
0.09 |
0.29 |
||
Ethyl Alcohol (Ethanol) - aq |
[162] |
-100.00 |
40.00 |
281.31 |
0.00 |
0.60 |
|
Melinder, Ethanol |
-44.00 |
20.00 |
261.15 |
0.11 |
0.60 |
||
Ethylene Glycol - aq |
[162] |
-100.00 |
100.00 |
304.88 |
0.00 |
0.60 |
|
Melinder, Ethylene Glycol |
-44.00 |
40.00 |
271.15 |
0.00 |
0.56 |
||
Glycerol - aq |
[162] |
-100.00 |
40.00 |
282.06 |
0.00 |
0.60 |
|
Melinder, Glycerol |
-40.00 |
40.00 |
273.15 |
0.20 |
0.63 |
||
MIT Seawater |
[183] |
0.00 |
120.00 |
333.15 |
0.00 |
0.12 |
|
Potassium Acetate (CH3CO2K) - aq |
[162] |
-100.00 |
40.00 |
279.93 |
0.00 |
0.45 |
|
Melinder, Potassium Acetate |
-44.00 |
30.00 |
266.15 |
0.11 |
0.41 |
||
Potassium Carbonate (K2CO3) - aq |
[162] |
-100.00 |
40.00 |
284.39 |
0.00 |
0.40 |
|
Melinder, Potassium Carbonate |
-35.00 |
30.00 |
270.65 |
0.00 |
0.39 |
||
Potassium Formate (CHKO2) - aq |
[162] |
-100.00 |
40.00 |
279.04 |
0.00 |
0.48 |
|
Lithium Chloride (LiCl) - aq |
[162] |
-100.00 |
40.00 |
274.64 |
0.00 |
0.24 |
|
Methyl Alcohol (Methanol) - aq |
[162] |
-100.00 |
40.00 |
276.69 |
0.00 |
0.60 |
|
Melinder, Methanol |
-50.00 |
20.00 |
258.15 |
0.08 |
0.47 |
||
MgCl2 - aq |
[162] |
-100.00 |
40.00 |
282.47 |
0.00 |
0.30 |
|
Melinder, Magnesium Chloride |
-30.00 |
30.00 |
273.15 |
0.00 |
0.21 |
||
Sodium Chloride (NaCl) - aq |
[162] |
-100.00 |
40.00 |
285.77 |
0.00 |
0.23 |
|
Melinder, Sodium Chloride |
-20.00 |
30.00 |
278.15 |
0.00 |
0.23 |
||
Propylene Glycol - aq |
[162] |
-100.00 |
100.00 |
305.86 |
0.00 |
0.60 |
|
Melinder, Propylene Glycol |
-45.00 |
40.00 |
270.65 |
0.15 |
0.57 |
||
VDI, Calcium Cloride |
-55.00 |
20.00 |
255.65 |
0.15 |
0.30 |
||
VDI, Potassium Carbonate |
-35.00 |
20.00 |
265.65 |
0.13 |
0.39 |
||
VDI, Methanol |
-80.00 |
0.00 |
233.15 |
0.10 |
0.90 |
||
VDI, Magnesium Chloride |
-33.00 |
20.00 |
266.65 |
0.07 |
0.21 |
||
VDI, Sodium Chloride |
-21.00 |
20.00 |
272.65 |
0.07 |
0.23 |
Name |
Description |
Reference |
\(T_\text{min}\) (°C) |
\(T_\text{max}\) (°C) |
\(T_\text{base}\) (K) |
\(x_\text{min}\) |
\(x_\text{max}\) |
|---|---|---|---|---|---|---|---|
ASHRAE, Ethylene Glycol |
-35.00 |
100.00 |
305.65 |
0.10 |
0.60 |
||
Antifrogen KF, Potassium Formate |
-40.00 |
50.00 |
278.15 |
0.40 |
1.00 |
||
Antifrogen L, Propylene Glycol |
-40.00 |
80.00 |
293.15 |
0.10 |
0.60 |
||
Antifrogen N, Ethylene Glycol |
-40.00 |
80.00 |
293.15 |
0.10 |
0.60 |
||
ASHRAE, Propylene Glycol |
-35.00 |
100.00 |
305.65 |
0.10 |
0.60 |
||
Glykosol N, Ethylene Glycol |
-53.00 |
100.00 |
296.65 |
0.10 |
0.60 |
||
Pekasol 2000, K acetate/formate |
-62.00 |
100.00 |
292.15 |
0.30 |
1.00 |
||
Pekasol L, Propylene Glycol |
-49.00 |
100.00 |
298.65 |
0.10 |
0.60 |
||
Zitrec AC, Corrosion Inhibitor |
0.00 |
100.00 |
323.15 |
0.06 |
0.50 |
||
Zitrec FC, Propylene Glycol |
-40.00 |
100.00 |
303.15 |
0.30 |
0.60 |
||
Zitrec LC, Propylene Glycol |
-50.00 |
100.00 |
298.15 |
0.30 |
0.70 |
||
Zitrec M, Ethylene Glycol |
-50.00 |
120.00 |
308.15 |
0.00 |
1.00 |
||
Zitrec MC, Ethylene Glycol |
-50.00 |
110.00 |
303.15 |
0.30 |
0.70 |
For slurry ice, the concentration \(x\) refers to the solid content and the heat capacity includes the heat of fusion. It might be necessary to adjust the solid content during heat transfer. The implementation is based on the data available in SecCool, which was originally recorded at the Danish Technological Institute (DTI).
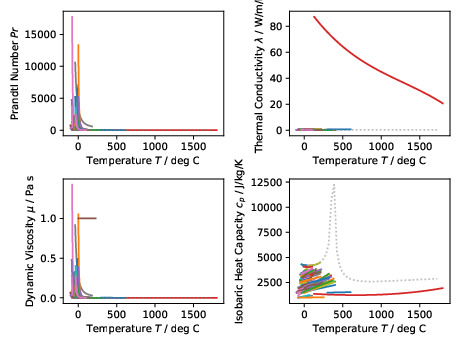
The figure above shows plots of the Prandtl numbers and associated fluid
properties for all incompressible fluids covering the whole temperature range
for each fluid. The original
PDF version
is also available for download.#
Adding New Fluids#
To add a fluid to the backend for incompressible fluids, you have to have the tabulated
property data available. Pure fluids are added to the PureFluids.py and binary
mixtures, like aqueous mixtures, have to be added to the SolutionFLuids.py.
The basic state variable for incompressible fluids is temperature, which should be provided as a one-dimensional numpy array with length \(N\). For pure fluids, all properties should match this temperature array in size since there is a 1-to-1 relation between the temperature points and the other quantities.
For binary mixtures, you also need a composition vector to define the data points properly. This composition vector is also a one-dimensional numpy array of the lenghth \(M\) and forms the second axis for your property space with \(N \times M\) data points.
Note that all properties have to have the same grid in terms of temperature and composition.
Once you haver added your fluid data, you can regenrate the JSON files with the fitted
parameters by running the script located at dev/incompressible_liquids/all_incompressibles.py.
Your new fluid is now part of the codebase and should be available to all CoolProp functions as
soon as you recompile the sources.
Remember that the incompressible fluids are prefixed with the backend name INCOMP when accessed
via the PropsSI function. If you define a new fluid called H2O2 in PureFluids.py, you
can use it later by typing INCOMP::H2O2.
